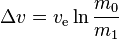Rocket equation and it's implications
Terminology
Thrust : In mechanical engineering, a normal reaction force applied perpendicular to the surface.
Effective exhaust velocity : It is same as actual exhaust velocity as long as we talk about ideal rocket equation.
It is an average velocity with which the burnt propellant and atmospheric oxygen leave the engine to produce the thrust which is equal to the thrust produced by an ideal jet exhaust.
Specific impulse : It's a term used to define engine efficiency of a rocket. Thrust generated per unit propellant flow rate.Greater the value of specific impulse,lower the value of propellant required to generate thrust.
Symbols used here have the obvious meanings. Just keep in mind that mass low rate is negative since the propellant is being expelled.
Tsialkovsky's rocket equation also known as ideal rocket equation is simple in the sense that it doesn't include gravitational field and assumes ideal condition for motion of a rocket i.e. no external forces act on the rocket.
Thrust : In mechanical engineering, a normal reaction force applied perpendicular to the surface.
Effective exhaust velocity : It is same as actual exhaust velocity as long as we talk about ideal rocket equation.
It is an average velocity with which the burnt propellant and atmospheric oxygen leave the engine to produce the thrust which is equal to the thrust produced by an ideal jet exhaust.
Specific impulse : It's a term used to define engine efficiency of a rocket. Thrust generated per unit propellant flow rate.Greater the value of specific impulse,lower the value of propellant required to generate thrust.
Tsialkovsky's rocket equation also known as ideal rocket equation is simple in the sense that it doesn't include gravitational field and assumes ideal condition for motion of a rocket i.e. no external forces act on the rocket.
It is still the basis of rocket dynamics.
where:
Is the initial total mass, including propellant
Is the final total mass without propellant, also known as dry mass.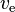
Is the effective exhaust velocity,
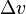Is delta-v - the maximum change of velocity of the vehicle (with no external forces acting),
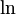refers to the natural logarithm function.
This equation gives the maximum change in velocity of a body that undergoes change in momentum by losing some amount of it's mass with high velocity.
I should have written my own interpretation but I thought this cannot get more clearer than this. So I took it directly from Wiki. Hope you don't mind it. :)
Derivation of the rocket equation
In practice, a jet engine is
characterized by its specific impulse Isp which is the time
expressed in seconds during which the engine provides a thrust of a kilogram
with a kilogram of propellant. In other words, it is the time during which the
engine provides an acceleration equal to Earth's gravity with one kilogram of
propellant. Longer is this time, more efficient is the engine.
The equation can also
be written using the specific impulse instead of the effective exhaust velocity by applying the formula
This
equation assumes that the specific impulse is constant in time, which is an
approximation since a rocket engine is more efficient in vacuum than at
atmospheric pressure. It doesn't take into account neither gravity field
(gravity losses) nor atmospheric resistance (drag losses).
When viewed as a variable-mass system(click here), a rocket cannot be directly analyzed with Newton's second law of motion because the law is valid for constant-mass systems only.It can cause confusion that the Tsiolkovsky rocket equation looks similar to the relativistic force equation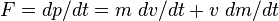 
. Using this formula with 
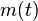as the varying mass of the rocket seems to derive Tsiolkovsky rocket equation, but this derivation is not correct. Notice that the effective exhaust velocity 
doesn't even appear in this formula.'' Ref. Wikipedia
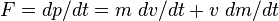. Using this formula with 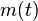as the varying mass of the rocket seems to derive Tsiolkovsky rocket equation, but this derivation is not correct. Notice that the effective exhaust velocity doesn't even appear in this formula.'' Ref. Wikipedia